Introduction à la théorie des ensembles
UE MATH : Logique et Arithmétique
Code de l'ECUE : SPUM202
PRESENTATION
Programme du cours:
Cet enseignement est en premier lieu destiné à des étudiants en licence qui souhaitent acquérir de meilleures compétences en raisonnement.
La première partie du cours a comme principal but de permettre aux étudiants d'améliorer leur faculté de raisonner.
Pour cela nous apprenons à utiliser un langage rigoureux dans la théorie des ensembles et nous apprenons les bases en logique pour pouvoir se lancer dans la pratique du raisonnement, fondamental en Mathématiques ainsi que dans d'autres sciences.
Ce cours revoit ensuite certaines questions déjà abordées au lycée, comme les applications et de l'arithmétique des entiers, et les enrichit.
Les relations généralisent la notion d'application. Nous étudierons en particulier les relations d'équivalence et les relations d'ordre, fondamentales en Structures Algébriques, en Analyse et en Théorie des Nombres.
Nous terminerons la première partie de ce cours par une introduction brève au dénombrement d'ensembles, revisitant les ensembles et les applications.
La deuxième partie de ce cours est dédiée à l'arithmétique des entiers et des polynômes.
La formalisation rigoureuse que nous adopterons sur l'arithmétique des entiers nous permettra de généraliser certaines notions et résultats à l'arithmétique des polynômes.
Dans une troisième partie, nous continuerons l'étude des nombres complexes, commencée dans le cours `Calculus II'. Nous étudierons en particulier l'arithmétique des polynômes complexes. Grâce à l'utilisation des nombres complexes, nous pourrons également étudier des problèmes de géométrie plane.
Certains thèmes ont déjà été abordés au lycée. Le but est ici de définir rigoureusement toutes les notions et d'insister sur les démonstrations.
Ce cours demande un investissement personnel conséquent (plusieurs heures de travail personnel par semaine), mais reste accessible à tous.
Responsable(s) du cours
, Ann LemahieuPrésentiel
- 24h de cours magistral
- 36h de travaux dirigés
PREREQUIS
-
Avoir envie d'apprendre à être rigoureux dans le syntaxe.
-
Avoir envie d'apprendre des concepts mathématiques abstraits en insistant sur les démonstrations plus que sur les calculs.
OBJECTIFS
- Connaître les bases en théorie des ensembles et savoir démontrer des propriétés sur les ensembles
- Utiliser les nombres complexes pour décrire et résoudre des problèmes en géométrie plane
- Manipuler la définition d'application et les propriétés injective, surjective, bijective, faire le lien avec le dénombrement
- Manipuler les définitions de relations d'équivalence et de relations d'ordre
- Appliquer les algorithmes relevant de l’arithmétique des entiers relatifs ou des polynômes : division euclidienne, calcul de pgcd, décomposition en facteurs irréductibles, résolution des équations de Bezout
- Mettre en œuvre des stratégies pour démontrer des propriétés arithmétiques des entiers ou des polynômes
- Expliquer les définitions relevant de l’arithmétique des entiers relatifs et des polynômes
- Utiliser les nombres complexes pour trouver les racines de polynômes de degré 2
CONTENU
-
Théorie des ensembles

-
Introduction à la logique

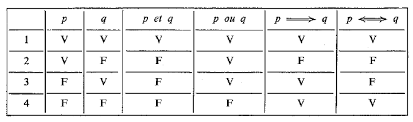
Assertions, tables de vérité, quantificateurs, types de raisonnement
-
Applications, relations, dénombrement

Applications : premières définitions, applications injectives, surjectives, bijectives
Relations : relations d'équivalence, partition, ensemble quotient ; relations d'ordre
Dénombrement : bases et lien avec les applications
-
Arithmétique des entiers

Divisibilité, nombres premiers, pgcd, rationalité et irrationalité, calcul modulaire...
-
Arithmétique des polynômes

Racines, arithmétique, théorème de D'Alembert-Gauss,
-
Nombres complexes

Racines de polynômes, nombres complexes et géométrie






