Il s'agit d'établir la définition de systèmes linéaires , de systèmes linéaires échelonnés .
La résolution de ces systèmes linéaires se fera en utilisant l'algorithme de Gauss , permettant de décrire complètement de façon algorithmique l'ensemble des solutions de ces systèmes.
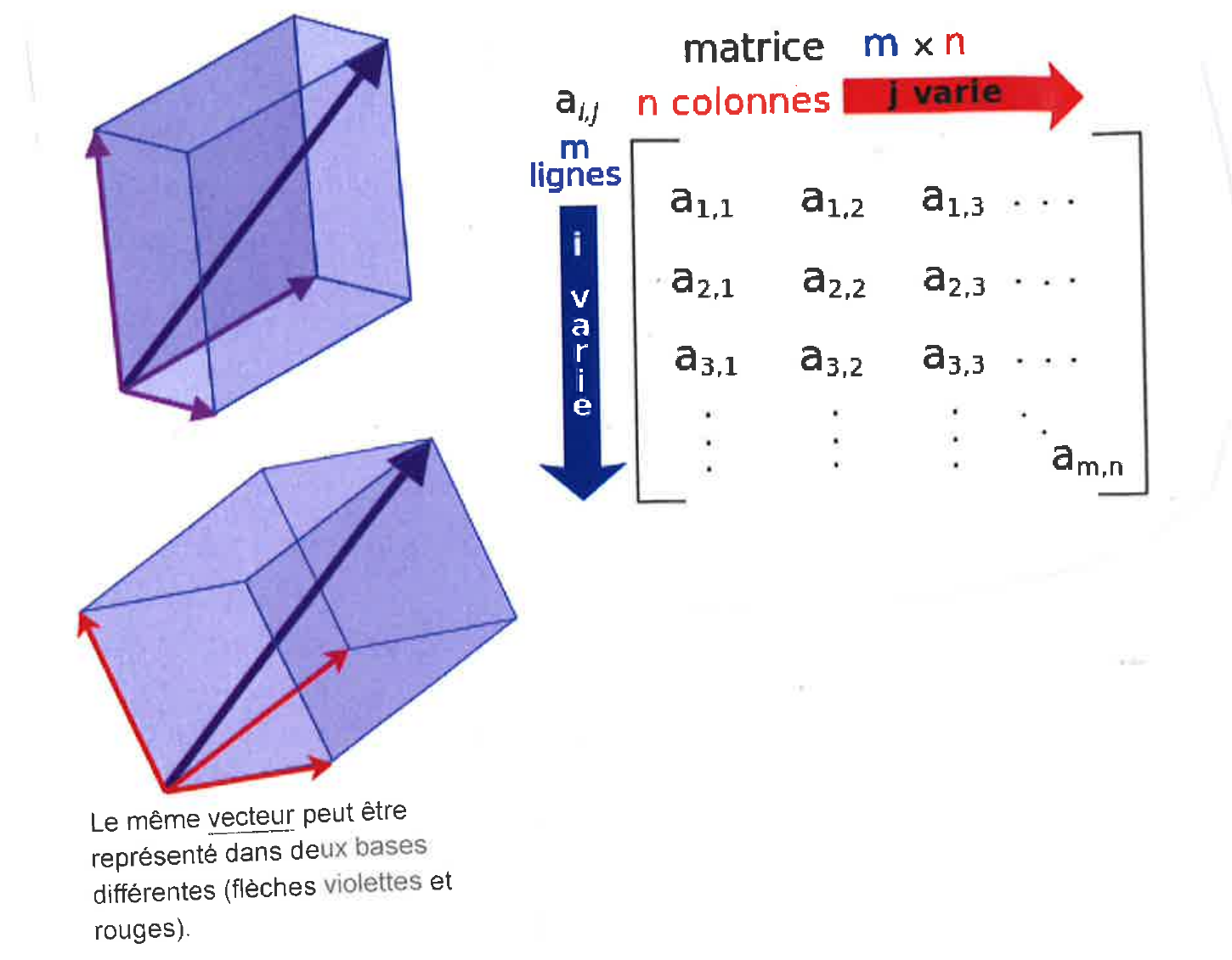
Nous apprendrons à effectuer ces calculs en travaillant sur la matrice augmentée du système qui allège la présentation des calculs.