ECUE Mathématiques 2

CONTENT

• Chapitre 1 Bases de R^n

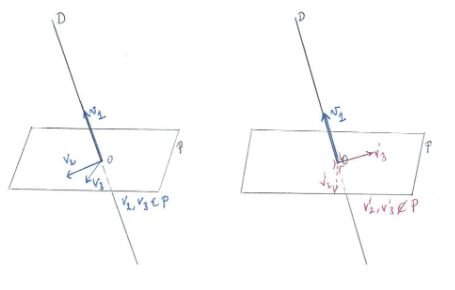
  On donne la définition des vecteurs de R^n, on rappelle les opérations élèmentaires que l'on peut faire sur les vecteurs, puis on définit la notion de combinaison linéaire et de base de R^n.

• Chapitre 2 Calcul matriciel

  On donne la définition des matrices, on rappelle les opérations élèmentaires que l'on peut faire sur les matrices, puis on définit la notion de matrice d'une famille de vecteurs et de matrice inversible.

• Chapitre 3 Systèmes linéaires

  On apprend à résoudre efficacement les systèmes d'équations linéaires. On applique cela à l'inversion des matrices carrées.

• Chapitre 4 Déterminant

  Dans ce chapitre, nous définissons le déterminant d'une famille de vecteurs et le déterminant d'une matrice. Nous apprenons à calculer ces déterminants, puis à les utiliser pour caractériser les bases de R^n et les matrices inversibles. Nous apprendrons aussi à calculer l'inverse d'une matrice ou les solutions d'un système linéaire en utilisant des déterminants.

• Chapitre 5 Valeurs propres, vecteurs propres et diagonalisation des matrices

  Dans ce chapitre, après avoir défini les notions de valeurs propres et vecteurs propres des matrices carrées, nous apprendrons à calculer les valeurs propres d'une matrice et à calculer les espaces propres associés. Puis nous étudierons les matrices diagonalisables et donneront des critères pratiques pour déterminer si une matrice est diagonalisable ou pas.

• Chapitre 6 Récurrences linéaires

  Dans ce chapitre, nous étudions les récurrences linéaires qui interviennent dans de nombreux modèles d'évolution dynamique discrets. Après avoir appris à les résoudre explicitement dans le cas où la matrice associée est diagonalisable, nous nous intéresserons à la détermination du comportement asymptotique du modèle dans le cas général, dans le cas diagonalisable et dans le cas des matrices positives (modèles de Perron Frobenius). Nous finissons le chapitre par l'étude des récurrences linéaires avec second membre.

• Chapitre 7 Optimisation des fonctions de plusieurs variables

  Dans ce chapitre, nous étudions les extrema de fonctions de plusieurs variables à valeurs réelles. Après avoir rappelé que ces extrema sont nécessairement atteints en des points critiques de la fonction, nous énonçons les conditions nécessaires et les conditions suffisantes vérifiées par la matrice Hessienne en un extremum local. Cette matrice est une matrice symétrique et ces conditions portent sur le signe des valeurs propres de ses valeurs propres. Il s'agit de la généralisation à un nombre quelconque de variables des résultats vus pour les fonctions de 2 variables en L1.

• Examen final
  No description