Université Côte d'azur
/ Formation / Syllabus SPUM30
Français English

UE MATHS S3 : Fondements 3

Code de l'ECUE : SPUM30

Ce cours donne droit à 6.0 ECTS.
PORTAIL SCIENCES ET TECHNOLOGIES
Mathématiques
Campus Valrose
Licence 2
Semestre impair
Français

PRESENTATION

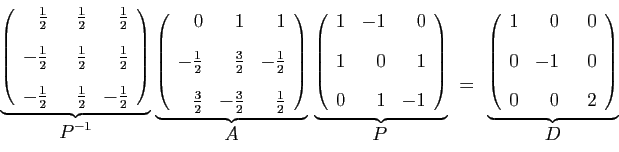
Dans la partie Algèbre de ce cours, nous abordons un problème classique en Algèbre linéaire : étant donné une application linéaire, nous nous proposons de chercher des bases dans lesquelles la forme de la matrice de l’application linéaire est la plus simple possible, en particulier diagonale.

Les techniques et les structures liées à ce problème ont des applications dans de nombreux domaines et nous en rencontrerons plusieurs dans ce cours. En plus des applications, nous apprendrons à comprendre et à faire des raisonnements en Algèbre linéaire.

Ce cours est destiné aux étudiants se dirigeant vers une licence mention Mathématiques, Informatique, Physique, Miashs et toute personne voulant acquérir les bases en Algèbre linéaire.

Certains aspects plus conceptuels ne seront pas approfondis dans ce cours. Les étudiants intéressés pourront les étudier en même temps dans l’UE Compléments d’Algèbre.

Dans la partie Analyse de ce cours, sont abordées les notions d’intégrale généralisée et de séries numériques, des concepts de base en Analyse.

Responsable(s) du cours

Ann Lemahieu , Simona Rotanodari

Présentiel

  • 24h de cours magistral
  • 48h de travaux dirigés

PREREQUIS

Avant le début du cours, je dois ...

OBJECTIFS

A la fin de ce cours, je devrais être capable de...
  • Démontrer des propriétés simples mettant en jeu les concepts de sommation.
  • Appliquer l'algorithme de Gauss pour calculer le rang d'une matrice et le déterminant d'une matrice carrée, pour calculer l'inverse d'une matrice et pour calculer les espaces propres d'une matrice/d'un endomorphisme.
  • Expliquer les définitions relevant de divers procédés de sommation "infinis" : nature des séries numériques (en étudiant la suite des sommes partielles), nature des intégrales généralisées (en étudiant la limite de primitives).
  • Appliquer l'algorithme de Gram-Schmidt pour calculer une base orthogonale.
  • Calculer la puissance n-ème d'une matrice diagonalisable pour prédire l'évolution d'un modèle biologique.
  • Restituer les démonstrations des principales propriétés dans l'étude des matrices/endomorphismes diagonalisables.
  • Démontrer de petites propriétés en mobilisant les définitions et les théorèmes appris relatifs à la réduction des endomorphismes.
  • Etudier la nature d'une série numérique et d'une intégrale généralisée en utilisant les définitions ou bien les critères basiques classiques (comparaison, équivalents, convergence absolue, etc.)

CONTENU

  • Dans la première séance nous rappelons les notions les plus importantes vues en Fondements Mathématiques 1 et Fondements Mathématiques 2. Nous introduisons aussi le déterminant pour une matrice carrée de dimension quelconque.

  • On fait quelques rappels sur le déterminant. On introduit la notion de rang d'une matrice et on étudie les systèmes linéaires à n équations et à n variables. 

  • Aucune description
  • Aucune description
  • Aucune description
  • Aucune description
Accéder au Syllabus complet (Authentification requise)
Important
Ce syllabus n’a aucune valeur contractuelle. Son contenu est susceptible d’évoluer en cours d’année : soyez attentifs aux dernières modifications.