Université Côte d'azur
/ Formation / Syllabus SPUM34
Français English

UE MATHS S3 : Méthodes - approche géométrique

Code de l'ECUE : SPUM34

Ce cours donne droit à 6.0 ECTS.
PORTAIL SCIENCES ET TECHNOLOGIES
Mathématiques , Mathématiques appliquées et applications des mathématiques
Campus Valrose
Licence 2
Semestre impair
Français

PRESENTATION

Ce cours est une généralisation des notions d'espaces vectoriels , de bases , d'applications linéaires , de produits scalaires .

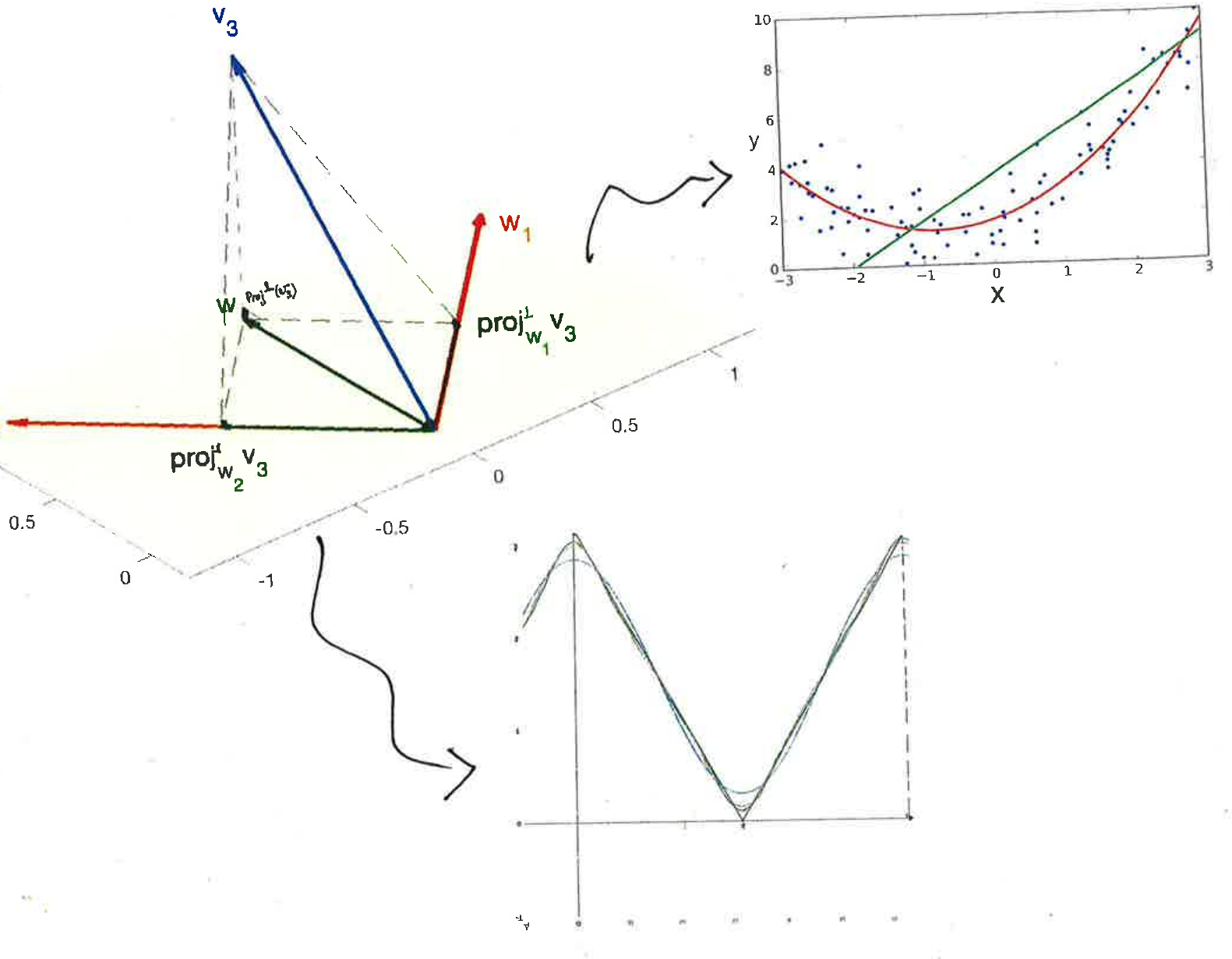
Ce cours présente enfin les espaces euclidiens et les applications de la projection orthogonale pour  établir la méthode d'approximation au sens des moindres carrés et les approximations de Fourier de fonctions.

Responsable(s) du cours

Mohamed El Kadi

Présentiel

  • 24h de cours magistral
  • 48h de travaux dirigés

PREREQUIS

Avant le début du cours, je dois ...
  • avoir suivi l'UE SPUM 22 sur les systèmes linéaires, les matrices, les espaces vectoriels R^n, la diagonalisation de matrices et les applications

OBJECTIFS

A la fin de ce cours, je devrais être capable de...
  • Projeter orthogonalement sur un sous-espace vectoriel dans un espace euclidien.
  • reconnaitre un espace vectoriel et reconnaitre un sous-espace vectoriel de R^n, des espaces de fonctions , des espaces de polynômes et des espaces de matrices.
  • Déterminer l'espace noyau et l'espace image d'une application linéaire. Appliquer le théorème du rang
  • Déterminer l'approximation au sens des moindres carré et approximation de Fourier
  • Construire des bases orthonormales à l'aide de l'algorithme de Gram-Schmidt dans des espaces euclidiens.
  • Reconnaitre si une famille de vecteurs est génératrice , libre ou si c'est une base.
  • Introduction aux formes quadratiques
  • Déterminer la matrice d'un endomorphisme Déterminer si l'application linéaire est une bijection

CONTENU

  • Définition d'espace vectoriel et définition de sous-espaces vectoriels de R^n et sous-espaces vectoriels  d'espaces de fonctions , de suites , de polynômes, de matrices.

  • Définition de bases  d' un espace vectoriel 

    Définition de dimension

    Somme directe d'espaces vectoriels

  • Matrice d'une application linéaire

    Déterminer la matrice d'une application linéaire dans une nouvelle base 

    Détermination des espaces noyau et image d'une apllication linéaire

    Application du théorème du rang

    Déterminer si une application linéaire est une bijection.

    Déterminer dans ce cas l'application inverse et la matrice de cette  application inverse. 

     

  • Définition d'un produit scalaire : exemples dans différents espaces vectoriels.

    Définition de bases orthonormales

    Construction de bases orthonormales par l'algorithme de Gram-Schmidt

    Définition de la projection orthogonale et Détermination du projeté orthogonal d'un vecteur sur un sous-espace vectoriel 

     approximation au sens de la norme minimale.

    Approximation au sens des moindres carrés

    Approximation de Fourier d'une fonction

  • Formes quadratiques , Lagrange

    Formes quadratiques définies positives, et négatives

Accéder au Syllabus complet (Authentification requise)
Important
Ce syllabus n’a aucune valeur contractuelle. Son contenu est susceptible d’évoluer en cours d’année : soyez attentifs aux dernières modifications.